Topic outline
-
In this course you will learn about:
- Plotting coordinates on the Cartesian plane.
- Finding the distance and midpoint of two points.
- Gradient of a line.
- Parallel and perpendicular lines.
-
Coordinate Geometry (also called analytical geometry) is the study of geometric objects and shapes (points, lines, quadrilaterals, etc.) on the Cartesian (coordinate) plane.
The Cartesian plane is a two-dimensional surface defined by two perpendicular number lines, which we call axes. The horizontal axis (running from left to right) is the x-axis and the vertical axis (running from top to bottom) is the y-axis. Each axis extends forever in both directions this is why we draw them with arrows on the ends.
We call the point where the axes meet the origin.
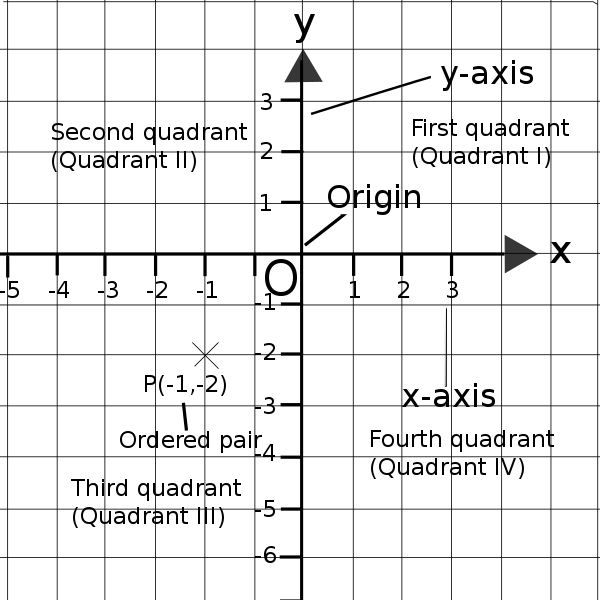
We can describe the position of any point on the Cartesian plane with an ordered pair. The first number is the x-coordinate (how far left or right of the origin the point is) and the second number is the y-coordinate (how far up or down from the origin the point is).
The Cartesian plane has four quadrants as shown in the diagram.
In the diagram we can see the point P with coordinates (-1; -2) is plotted in the third quadrant. The point P is 1 unit to the left from the origin and 2 units down from the origin.
Try the next activity to test your knowledge on plotting points by dragging the coordinates to the letters on the Cartesian plane.
-
Exercise: Plot points from a table
1. Plot the coordinate pairs shown in the table.
2. Join the dots. What do you notice?
3. Find an equation that relates \(x\) to \(y\).
Solution
2. If we join the dots we see that the points all lie on the same straight line as shown in the diagram.
3. The equation that relates \(x\) to \(y\) is \(y=x+1\).
-
-
Distance Formula
To calculate the distance between two points \( ({x}_{1}, {y}_{1}) \) and \( ({x}_{2}, {y}_{2}) \) we use the formula:
\(d=\sqrt { ({{x}_{1}-{x}_{2} })^{ 2}+({y}_{1}-{y}_{2})^{2} }\)
It does not matter which point we assign as point \(1\) and which we assign as point \(2\). Watch the next video to learn how to apply the distance formula.
Midpoint formula
To calculate the coordinate of the midpoint between two points \( ({x}_{1}, {y}_{1}) \) and \( ({x}_{2}, {y}_{2}) \) we use the formula:
\(Midpoint=(\frac{{x}_{1}+{x}_{2}}{2}, \frac{{y}_{1}+{y}_{2}}{2})\)
In the next video you will learn to apply the midpoint formula.
After watching both videos try the exercises that follow to test your knowledge on the distance and midpoint formulas.
-
Exercise: Practise using the distance and midpoint formulae
Try the exercise Midpoint Formula to practise your skills.
Try the exercise Distance between points to practise your skills.
-
-
How to find the gradient of a line
Gradient is a measure of the steepness of a line.
We use the formula \(m=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}\) to calculate the gradient or slope between any two points on a straight line.
Example
Find the gradient between the points \(A(5,2)\) and \(B(9,-3)\).
\({m}_{AB}=\frac{-3-2}{9-5}=\frac{-5}{4}\)
Note: If you start with \({y}_{2}\) in the numerator then you must start with \({x}_{2}\) in the denominator. If you change the order you start with then the answer will not be correct.
Watch the next video for further explanation on finding the gradient.
If you would like more practise finding the gradient between two points, visit the interactive simulation called Calculating gradient. Choose any two points on the Cartesian plane and click on "show calculation" to see how the gradient is worked out.-
Parallel and perpendicular lines
Parallel lines are always the same distance apart. This means that on the Cartesian plane, parallel lines have the same gradient. So to show that two lines are parallel we simply need to show that their gradients are equal.
Perpendicular lines lie at \({90}^\circ\) to each other. If two lines are perpendicular then the product of their gradients is \(-1\).
In the next video you will go over a few examples using the gradients of parallel and perpendicular lines.
-