Topic outline
-
Outcomes
In this course you will learn about:
- Angles and lines.
- Angles formed between parallel lines.
- Classifying polygons.
- Quadrilaterals.
-
An angle is formed when two lines meet or intersect at a point (called a vertex). We measure the size of the angle between the two lines in degrees. Here is some of the basic terminology used to describe and work with angles.
- Angles smaller than \({90}^\circ\) are called acute angles.
- Angles equal to \({90}^\circ\) are called right angles.
- Angles between \({90}^\circ\) and \({180}^\circ\) are called obtuse angles.
- Angles of \({180}^\circ\) are called straight angles and are on a straight line.
- Angles between \({180}^\circ\) and \({360}^\circ\) are called reflex angles.
- Angles that add up to \({90}^\circ\) are called complementary angles.
- Angles that add up to \({180}^\circ\) are called supplementary angles.
- If two straight lines intersect each other, four angles are created. The vertically opposite angles in this case are equal. In the diagram below, \(\angle\( {A}_{1} \)=\angle\( {A}_{2} \)=\angle\( {A}_{3} \)=\angle\( {A}_{4}\)\).
For a visual summary of the special lines and angles discussed, watch the next video.
Try the activity on Geometry of straight lines to make sure you understand the different types of angles formed on straight lines.-
Exercise: Constructions
You will need a compass, a set square and a pencil for the constructions.
Constructing a perpendicular line
Watch the next video to learn two different methods for constructing a perpendicular line.
Bisecting an angle
The next video shows you how to bisect an angle using a compass and a ruler.
Constructing a parallel line to a given line
-
When two lines are cut by a transversal, corresponding, alternate and co-interior angles are always created. A line that intersects other lines is called a transversal. In the figure below, EF is a transversal intersecting the lines AB and BC.
If the lines being cut by the transversal are parallel, then the corresponding angles are equal, the alternate angles are equal and the co-interior angles are supplementary.
By the same logic, if the corresponding angles are equal, or the alternate angles are equal or the co-interior angles are supplementary, then the lines are parallel.
For a summary of the angles created by parallel lines and to see which angles are equal, watch the video called Angles In Parallel Lines.
Complete the next exercise to test your knowledge.-
Exercise: Find angles between parallel lines
Complete the exercise Parallel lines to check that you understand how to find unknown angles between parallel lines.
-
-
Some of the common shapes that you may have seen are triangles, rectangles, hexagons and squares. The name we give to these types of shapes, formed with straight lines and that can be drawn on a flat (two-dimensional) surface is polygons.
A polygon is named according to the number of sides it has, it can have three or more sides. The names are based on the prefixes of Greek numbers. In fact, you will find references to Greek numerical prefixes in many everyday objects and this can help you remember the number of sides a polygon has. For example, a decade is 10 years and a decagon has 10 sides; an octopus has eight legs and an octagon has eight sides. Can you think of other examples that use Greek numerical prefixes?
The figure below shows the different types of polygons that you may come across and examples of shapes that are not polygons.

-
Introduction to quadrilaterals
A quadrilateral is any flat, four-sided figure. Each of the four sides must be straight. A square is an example of a quadrilateral, so is a parallelogram. These are very special kinds of quadrilaterals with special properties.
The figure below shows various examples of quadrilaterals.
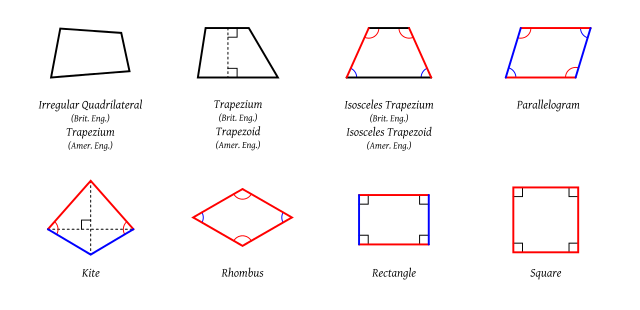
To learn about the properties of the special quadrilaterals watch the next video.
-