Topic outline

  • Outcomes

    Collapse all Expand all


    In this course you will learn about:

    1. Properties of similar triangles.
    2. Conditions for similarity.
    3. Proving triangles similar.

  • Properties of similar triangles

    Shapes that are similar look the same but differ in size while congruent figures have the same shape and the same size. 

    Note: all congruent triangles are similar but not all similar triangles are congruent

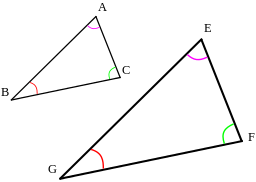
    In similar triangles the corresponding angles are equal and the corresponding sides are in proportion.

    The next video shows what it means for triangles to be similar and discusses the basic facts you need to know about similar triangles. 

    • Order matters

      We use the symbol \(|||\) or \(\sim\) to show that shapes are similar. If \(∆XYZ\) is similar to \(∆PQR\), then we write: \(∆XYZ |||∆PQR\) or \(∆XYZ\sim∆PQR\).

      The order of the letters in the notation of similar triangles indicates which angles and sides are equal and it is extremely important to name the triangles using the correct vertex order.

      Given that \(∆XYZ|||∆PQR\) this would them imply that:

      Angles: \(X=P\) and \(Y=Q\) and \(Z=R\) 

      Sides: \(\frac{XY}{PQ}=\frac{XZ}{PR}=\frac{YZ}{QR}\)

      If the triangles’ vertices were written in a different order, then the statements above would not be true.


    • Quiz icon
      Notation used in similarity Quiz
    • H5P icon
      Similar or congruent? H5P

  • Conditions for similarity

    There are three ways to prove similarity:

    1. If two triangles have two angles equal to each other, then the triangles are similar (when two angles are equal then all three angles must be equal). We use \(AAA\) to show this relationship
    2. If two triangles have three pairs of sides in the same ratio, then the triangles are similar
    3. If two triangles have two pairs of sides in the same ratio and the included angles are also equal, then the triangles are similar. We use the letters \(SAS\) to show that relationship.
    Watch the video to see these three postulates (statement that is taken to be true without proving it) in action.

  • Proving triangles are similar

    In the following video examples we will explore the different ways we can prove that triangles are similar using the conditions for similarity. 

    Make sure to pause the video and attempt the questions for yourself before the solution is shown.