Topic outline
-
-
-
Mass and inertia
If you took a physics textbook, with a weight of 10 newtons, into space, it would become weightless, but it would still have the same mass.
The mass of an object is the amount of matter in it. It is measured in kilograms.
When an object is stationary, it needs a force to make it move. The bigger the mass, the bigger the force needed to make it move. We say masses have inertia, a reluctance to start moving.
Activity 1

1. Hang two tins from a long piece of string.
2. Fill one tin with wet sand or stones and leave the other empty.
3. Try pushing the cans.
Which can is harder to push?
Which can has the larger inertia?
Which can has the larger mass?
Since the experiment depends on the mass of the object and not the weight, you would feel the same effect on the Moon or out in space – if you push a large mass you would feel a large amount of inertia.
In a similar way, moving objects need a force to stop them moving. Their inertia tends to keep them moving.
Activity 2
1. Using the cans from activity 1 – push them to get them moving.
2. Try to stop them moving with your hand.
Which can is harder to stop?
Passengers in a car have a lot of inertia and so they need seatbelts. If the car stops suddenly, the people will tend to keep moving (even through the windscreen) unless the seatbelts exert a large force to stop them.

What happens when the car you are travelling in turns a corner? Your body, because of its inertia, will tend to travel straight on. You can feel your body sway as the car turns, but fortunately your car seat exerts a force on you and this pulls your round the corner with the car.
Newtons first law of motion:


Examples of objects with uniform motion
Newton's first law can be used to explain the movement of objects travelling with uniform motion (constant velocity). For example, when a car travels at a constant velocity, the driving force from the engine is balanced by the resistive forces such as air resistance and frictional forces in the car's moving parts. The resultant force on the car is zero.
Other examples include:
a runner at their top speed experiences the same air resistance as their thrust
an object falling at terminal velocity experiences the same air resistance as its weight
If the forces acting on an object are balanced, the resultant force is zero.
Examples of objects with non-uniform motion
Newton's first law can also be used to explain the movement of objects travelling with non-uniform motion. This includes situations when the speed changes, the direction changes, or both change. For example, when a car accelerates, the driving force from the engine is greater than the resistive forces. The resultant force is not zero.
Other examples include:
at the start of their run, a runner experiences less air resistance than their thrust, so they accelerate
an object that begins to fall experiences less air resistance than its weight, so it accelerates
If the forces acting on an object are not balanced, the resultant force is not zero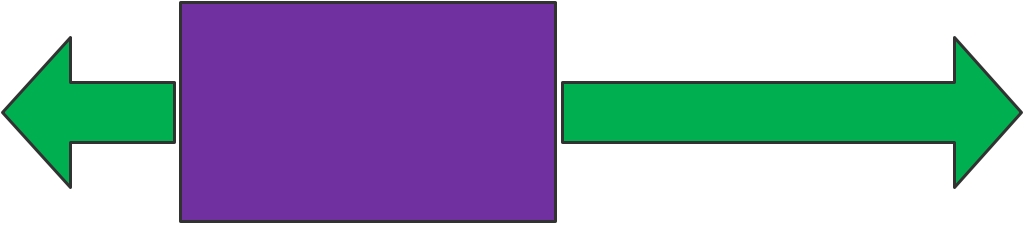
-
-
-
Force, mass and acceleration
When the forces on an object are unbalanced, there is a resultant force. This resultant force cause the object to change its velocity. It will accelerate or decelerate.
The bigger the force on the object, the more it accelerates.
The heavier the object, the less it accelerates.
Newton's second law of motion can be described by this equation:
resultant force = mass × acceleration
F = ma
This is when:
- force (F) is measured in newtons (N)
- mass (m) is measured in kilograms (kg)
- acceleration (α) is measured in metres per second squared (m/s2)
The equation shows that the acceleration of an object is:
- proportional to the resultant force on the object
- inversely proportional to the mass of the object
In other words, the acceleration of an object increases if the resultant force on it increases, and decreases if the mass of the object increases.
One newton (1 N) is defined as the force which gives to a mass of 1 kg, an acceleration of 1 m/s2.
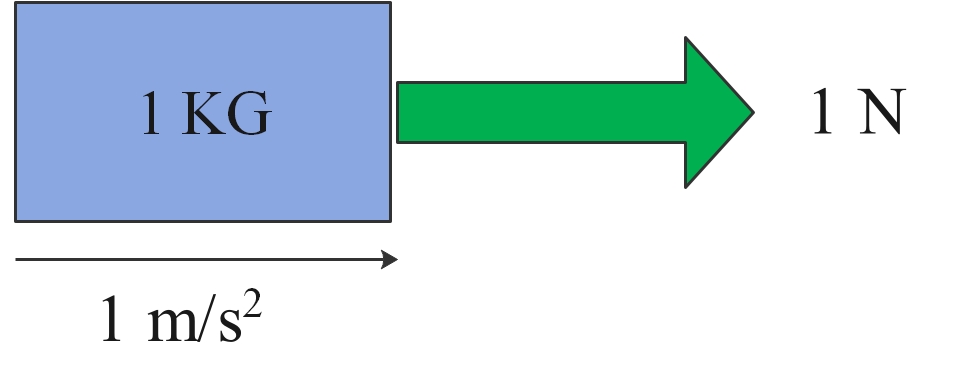
Example:
Calculate the force needed to accelerate a 22 kg cheetah at 15 m/s2.
F = 22 x 15
F = 330 N
Example:
Calculate the force needed to accelerate a 15 kg gazelle at 10 m/s2.
F = ma
F = 15 x 10
F = 150 N- Newton's second law: Force = change in momentum/time taken = rate of change of momentum
-
Investigating acceleration
Investigate the relationship between the force, mass and acceleration by varying the masses added to trolleys
More than one method could be used to investigate the relationship between the force, mass and acceleration. This method will vary the masses added to trolleys.
Aim of the experiment
To investigate the relationship between the force, mass and acceleration by varying the masses added to trolleys.
Method
The video shows apparatus that can used in this investigation.
- Set up the equipment. Make sure that the track is level, and that the card will pass through both gates before the masses strike the floor.
- Use scales to measure the total mass of the glider, string and weight stack. Record this value.
- Attach the full weight stack (6 x 10g masses) to the end of the string.
- Make sure the trolley is in position. Push the trolley.
- Remove one weight and attach it to the trolley using blu-tack. This will keep the total mass constant. (The weight stack is being accelerated too.)
- Repeat steps 6-7 removing one weight from the stack each time. Remember to attach each weight to the trolley as it is removed from the weight stack.
Results
Record the results in a suitable table, similar to the example results below:
Number of weights on stack Force in N Acceleration in m/s² - Run 1 Acceleration in m/s² - Run 2 Acceleration in m/s² - Run 3 Acceleration in m/s² - Mean 6 0.6 2.90 2.95 3.05 2.97 5 0.5 2.21 2.36 2.26 2.28 4 0.4 1.93 1.78 1.83 1.85 3 0.3 1.65 1.54 1.49 1.56 2 0.2 1.32 1.27 1.42 1.34 1 0.1 1.16 1.11 1.26 1.18 Analysis
- Plot a scatter graph with force on the vertical axis, and acceleration on the horizontal axis. Draw a suitable line of best fit.
- Describe what the results show about the effect of increasing the force which is accelerating the object.
- Extension: calculate the gradient of your graph and compare this to the to total mass of the glider and weight stack measured in step 4 above.
Evaluation
Acceleration is direcly proportional to the force applied to the object. This means that a graph of force against acceleration should produce a straight line that passes through the origin.
To what extent do your results show this relationship? For example, do all your points lie on a straight line passing through the origin, or are there any anomalous points?
-
-
-
Elastic and inelastic collisions
Momentum, kinetic energy and impulse can be used to analyse collisions between objects such as vehicles or balls. Forces and the final velocity of objects can be determined.
Elastic vs inelastic collision is a comparison of two types of collisions that differ in the conservation or loss of kinetic energy.
In an elastic collision, the total kinetic energy of the colliding objects is the same before and after the collision. In an inelastic collision, the total kinetic energy of the objects is less after the collision than before, and some energy is changed into other forms like heat, sound, or radiation.
Another way to distinguish elastic and inelastic collisions is by looking at whether the objects are stuck together or moving separately before and after the collision. If the objects are stuck together either before or after the collision, the collision is inelastic; if the objects start and end moving separately from each other, the collision is elastic.
If kinetic energy before is the same as after, then the collision is elastic. Interactions between molecules are examples of perfectly elastic collisions. In most other cases (eg snooker balls), collisions are not perfectly elastic - some kinetic energy is lost. But this must be tested by calculation.
Kinetic energy can be calculated using the following equation:
Ek = 1/2 mv2
When working with collisions, kinetic energy must be worked out for each object involved both before and after the collision.
Question:
If two bumper cars collide head-on in a fairground and both cars come to a stop due to the collision, kinetic energy is obviously not conserved. Is momentum conserved even though both cars stop?
Answer:
Yes, although there is no momentum after the collision, there was no total momentum before the collision. Momentum is a vector quantity. The positive momentum of one car must have been balanced out by the negative momentum of the other car.
Question:
Is kinetic energy conserved even though both cars stop?
Answer:
No. Kinetic energy is a scalar quantity so there is no balancing out of the different directions. Both cars were moving and had kinetic energy before the collision. Both cars are at rest and have no kinetic energy after.
Question A red snooker ball and a blue snooker ball (each with a mass of 160 g) collide. The red ball is travelling from left to right at 0.28 m/s. The blue ball is travelling from right to left at 0.12 m/s. This is shown in the diagram below. 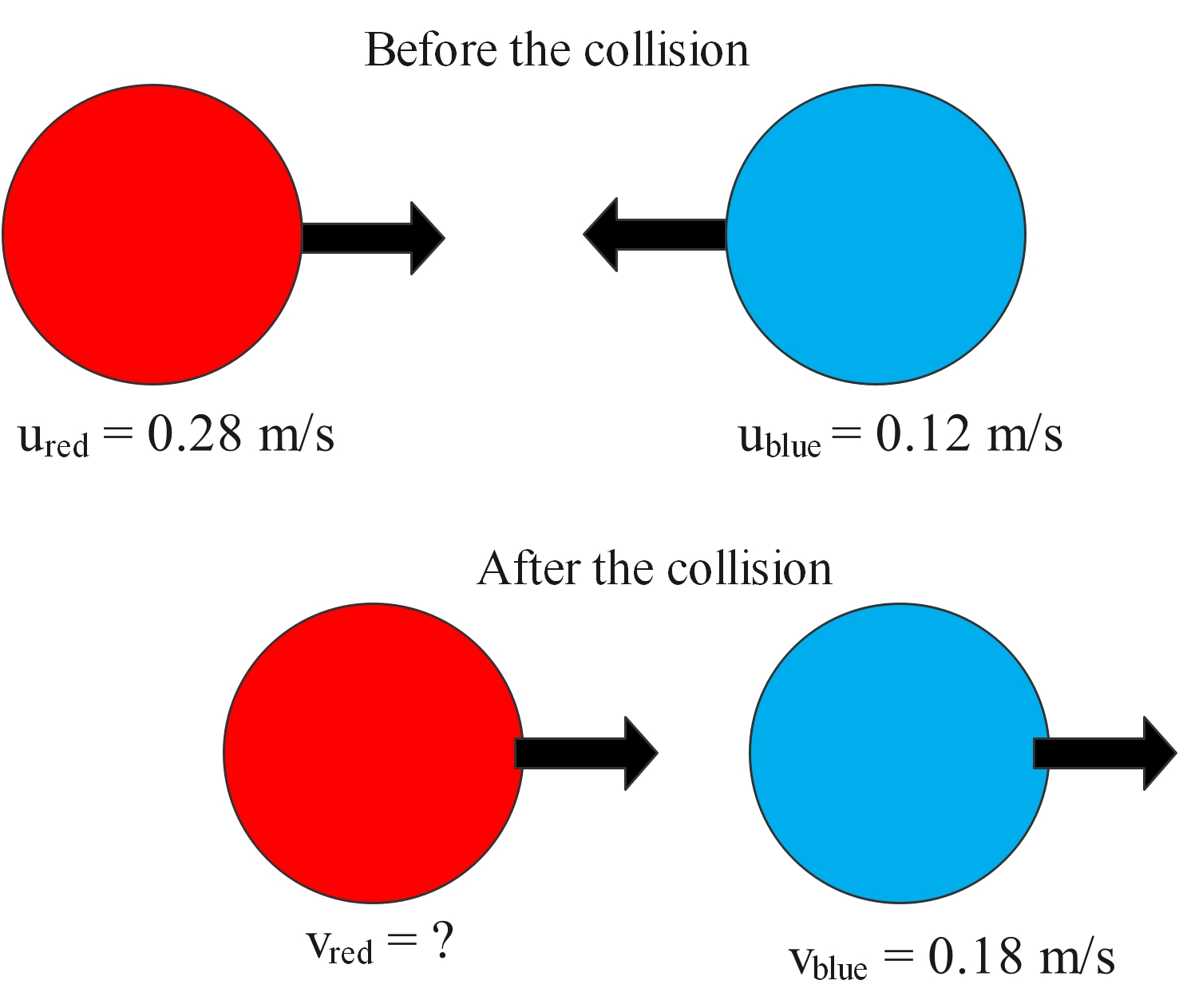
After the collision, the blue ball travels from left to right at 0.18 ms-1. a) Calculate the velocity of the red ball after the collision. b) Use kinetic energy to determine whether the collision was elastic or not. Answer: a) Total momentum before = total momentum after mredured + mblueublue = mredured + mblueublue 0.16 × 0.28 + 0.16 × (−0.12)= 0.16× vred + 0.16 × 0.18 Rearranging: 0.16× vred =(0.0448−0.0192) − 0.0288 =0.0256−0.0288 =−0.00320.16 vred =−0.02 m/s. This is a negative value, so the direction is from right to left. b) To determine if the collision is elastic or not, you must work out the kinetic energy before and after the collision. This example deals with two objects. The kinetic energy before the collision involves their initial speed. The kinetic energy before the collision is 0.00742 J The kinetic energy after the collision is 0.00262 J So the total kinetic energy lost is 0.0048 J The collision is inelastic. -
Linear Momentum
Momentum
Momentum is the product of a moving object's mass and velocity.
Momentum = mass x velocity
The symbol for momentum is p
so this can also be written as: p = mv
Momentum is measured in kg ms-1.
Momentum is a vector quantity that depends on the direction of the object. Momentum is of interest during collisions between objects.
When two objects collide the total momentum before the collision is equal to the total momentum after the collision (in the absence of external forces).
This is the law of conservation of momentum. It is true for all collisions.
Conservation of momentum example
Consider two model cars of mass 1.2 and 1.4 kg colliding at the speeds shown:
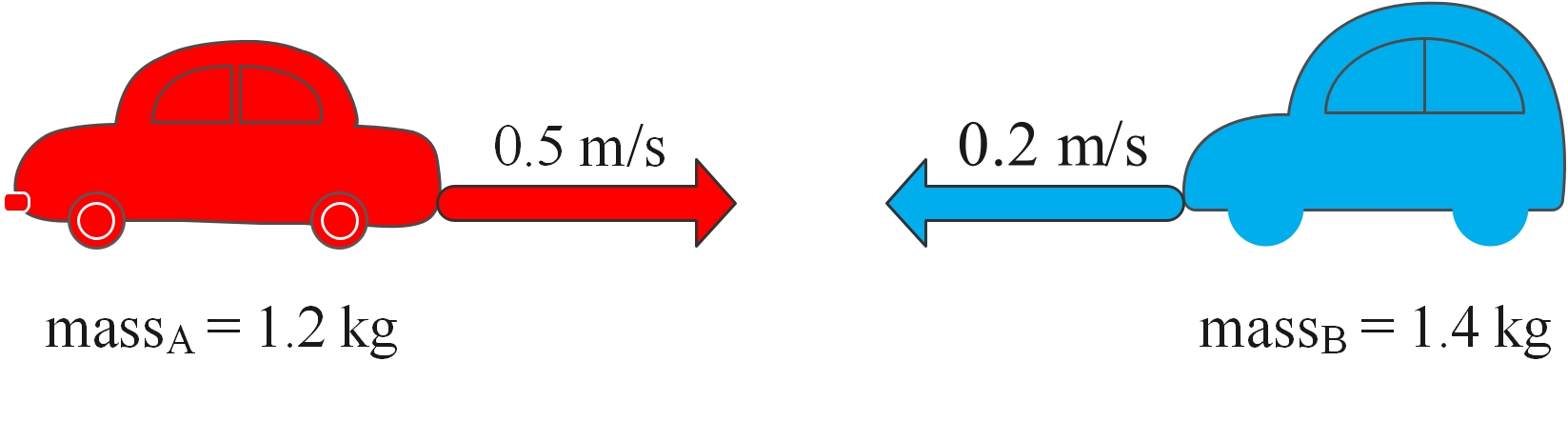
The total momentum before the collision is the sum of both momentums:
Momentum of red car A:
p = mAv
1.2 x 0.5
= 0.6 kg m/s
Momentum of red car B:
p = mBv
1.4 x 0.2
= 0.28 kg m/sThe blue car is travelling in the negative direction, so the momentum is subtracted.
Total momentum:
0.6 - 0.28
= 0.32 kg m/s
If the two cars stick together after the collision and move as one, then the velocity of the two cars can be determined because the total momentum after the collision is the same (ie 0.32 kg m/s).
The total mass is now 2.6 kg.
Total momentum after collision is 0.32 kg m/s:
0.32 = mAB x vAB
0.32 = 2.6 x vAB
vAB = 0.32/2.6
= 0.12 m/s
The velocity is positive, so this shows that the two cars move off in the positive (left to right) direction.
- The total momentum of two objects before a collision is the same as their total momentum after the collision - provided there are no external forces.
- Momentum is conserved in a collision, but kinetic energy is not.
- Momentum (kg m/s) = mass (kg) x velocity (m/s). It is a vector quantity
- Principle of conservation of momentum: total momentum before collision = total momentum after collision
-
-
-
According to Newton's third law of motion, whenever two objects interact, they exert equal and opposite forces on each other.
This is often worded as 'every action has an equal and opposite reaction'. However, it is important to remember that the two forces:
- act on two different objects
- are of the same type (eg both contact forces)
Examples of force pairs
Newton's third law can be applied to examples of equilibrium situations.

When the mountain climber pulls down on the rope, the rope pulls up on the mountain climber.
A cat sits on the ground
There are contact gravitational forces between Earth and the cat:
- the cat pulls the Earth up
- the Earth pulls the cat down
These forces are equal in size and opposite in direction.
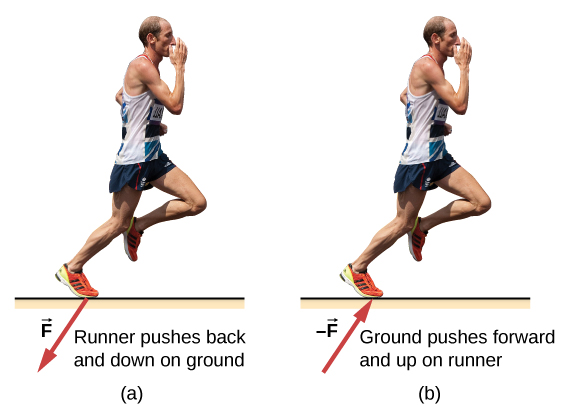
The runner experiences Newton’s third law. (a) A force is exerted by the runner on the ground. (b) The reaction force of the ground on the runner pushes him forward.
Pushing a pram
There are contact forces between the person and the pram:
- the person pushes the pram forwards
- the pram pushes the person backwards
These forces are equal in size and opposite in direction.
Car tyre on a road
There are contact forces between the tyre and the road:
- the tyre pushes the road backwards
- the road pushes the tyre forwards
These forces are equal in size and opposite in direction.
A satellite in Earth orbit
There are non-contact gravitational forces between Earth and the satellite:
- the Earth pulls the satellite
- the satellite pulls Earth
These forces are equal in size and opposite in direction.
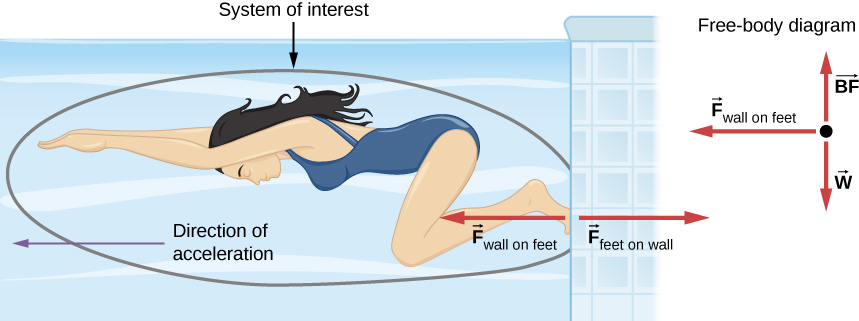
When the swimmer exerts a force on the wall, she accelerates in the opposite direction; in other words, the net external force on her is in the direction opposite of F feet on wall. This opposition occurs because, in accordance with Newton’s third law, the wall exerts a force F wall on feet on the swimmer that is equal in magnitude but in the direction opposite to the one she exerts on it. The free-body diagram shows F wall on feet w (the gravitational force), and BF, which is the buoyant force of the water supporting the swimmer’s weight. The vertical forces w and BF cancel because there is no vertical acceleration.
-