Topic outline
-
In this course you will learn about:- Enlargement and reduction of shapes using a scale factor.
- Reflection of geometric shapes.
- Translation of geometric shapes.
- Rotation of geometric shapes.
-
Enlargement or reduction of a geometric figure transforms (changes) its size but not the shape of the figure. We call this a non-rigid transformation. The enlarged or reduced shape is called the "image" of the original shape.
We multiply each side of the original shape by a scale factor to produce the enlarged or reduced image. Maps make use of scale factors to reduce the size of a geographical area, can you think of other real life uses of scale factors?
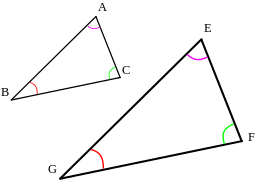
We can say that triangle EGF is an enlargement of triangle ABC or that triangle ABC is a reduction of triangle EGF.
-
Enlargement and reduction
The image and the original shape that was transformed are similar since their corresponding angles are all equal.
In the next video you will learn how to work out scale factors, and to find the lengths of the sides of the image if you are given the scale factor.
-
-
There are two types of transformations; rigid transformations and non-rigid transformations. A rigid transformation is one in which the original shape and the image have the same size and shape. Reflections are an example of rigid transformations.

A reflection "flips"an object over a line. Think about looking in a mirror, you see a reflection of yourself. In Maths instead of a mirror we use a mirror line to reflect objects and points. In the next video you will see examples of reflections and how to perform this transformation.
-
A translation is a moving or sliding of an image or point either in a vertical direction, horizontal direction, or in both a vertical and horizontal directions. It is a rigid transformation as shape and size are maintained.
In the next video you will learn how to translate shapes on a grid.
After watching the video try the Translate shapes exercise and then the quiz that follows next. -
A rotation is a transformation that "turns" an object around a fixed point, called the center of rotation. It is a rigid transformation as shape and size are maintained.
In a rotation an object is turned around a centre point. The distance from the centre to any point on the shape/object stays the same. Remember to always state the angle and direction of the rotation.
In the next video you will be taken through an example of how to perform a rotation on an axis. Make sure to have a ruler and pencil ready.
-
Practise rotating images
Try this exercise to test your understanding of rotating around a point: Rotate Shapes. If you need more help on rotating shapes watch the video below.
-